Advertisements
Advertisements
प्रश्न
Let A = {1, 2, 3}. Write all one-one from A to itself.
उत्तर
A ={1, 2, 3}
Number of elements in A = 3
Number of one-one functions = number of ways of arranging 3 elements = 3! = 6
(i) {(1, 1), (2, 2), (3, 3)}
(ii) {(1, 1), (2, 3), (3, 2)}
(iii) {(1, 2 ), (2, 2), (3, 3 )}
(iv) {(1, 2), (2, 1), (3, 3)}
(v) {(1, 3), (2, 2), (3, 1)}
(vi) {(1, 3), (2, 1), (3,2 )}
APPEARS IN
संबंधित प्रश्न
Show that the modulus function f: R → R given by f(x) = |x| is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is − x if x is negative.
Show that the function f: R → R given by f(x) = x3 is injective.
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
F = {(a, 2), (b, 1), (c, 1)}
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x2
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x2
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
` if f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.
If f : Q → Q, g : Q → Q are two functions defined by f(x) = 2 x and g(x) = x + 2, show that f and g are bijective maps. Verify that (gof)−1 = f−1 og −1.
Let f be a function from R to R, such that f(x) = cos (x + 2). Is f invertible? Justify your answer.
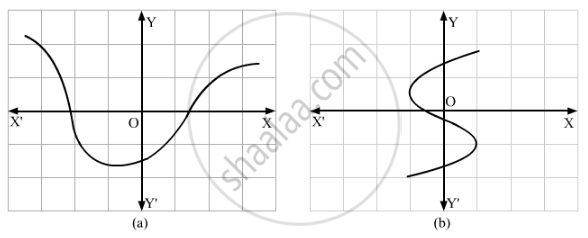
Which one of the following graphs represents a function?
Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
If f : R → R is defined by f(x) = x2, find f−1 (−25).
Let A = {1, 2, 3, 4} and B = {a, b} be two sets. Write the total number of onto functions from A to B.
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
Let
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
If \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to
Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.
Let
\[f : R \to R\] be given by \[f\left( x \right) = x^2 - 3\] Then, \[f^{- 1}\] is given by
Let A = R − (2) and B = R − (1). If f: A ⟶ B is a function defined by`"f(x)"=("x"-1)/("x"-2),` how that f is one-one and onto. Hence, find f−1.
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Let A be a finite set. Then, each injective function from A into itself is not surjective.
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
k(x) = x2
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is ____________.
Let f: R → R defined by f(x) = x4. Choose the correct answer
Let f: R → R defined by f(x) = 3x. Choose the correct answer
If `f : R -> R^+ U {0}` be defined by `f(x) = x^2, x ∈ R`. The mapping is
Let f: R→R be a continuous function such that f(x) + f(x + 1) = 2, for all x ∈ R. If I1 = `int_0^8f(x)dx` and I2 = `int_(-1)^3f(x)dx`, then the value of I1 + 2I2 is equal to ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
