Advertisements
Advertisements
प्रश्न
Which one of the following graphs is a function of x?
 |
 |
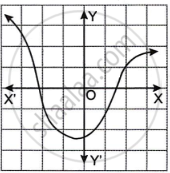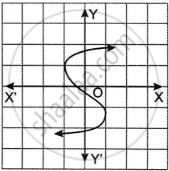| Graph A | Graph B |
Advertisements
उत्तर
Graph A represents the function of x.
In graph B, we see that for a value of x, there are 2 values of y.
APPEARS IN
संबंधित प्रश्न
Show that the function f : R* → R* defined by f(x) = `1/x` is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true, if the domain R* is replaced by N with co-domain being same as R?
Check the injectivity and surjectivity of the following function:
f : R → R given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f : N → N given by f(x) = x3
Let f : R → R be defined as f(x) = x4. Choose the correct answer.
Show that the logarithmic function f : R0+ → R given by f (x) loga x ,a> 0 is a bijection.
Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 8x3 and g(x) = x1/3.
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
Let
f (x) =`{ (1 + x, 0≤ x ≤ 2) , (3 -x , 2 < x ≤ 3):}`
Find fof.
A function f : R → R is defined as f(x) = x3 + 4. Is it a bijection or not? In case it is a bijection, find f−1 (3).
Let f, g : R → R be defined by f(x) = 2x + l and g(x) = x2−2 for all x
∈ R, respectively. Then, find gof. [NCERT EXEMPLAR]
The function
f : A → B defined by
f (x) = - x2 + 6x - 8 is a bijection if
If the function
\[f : R \to R\] be such that
\[f\left( x \right) = x - \left[ x \right]\] where [x] denotes the greatest integer less than or equal to x, then \[f^{- 1} \left( x \right)\]
If \[f\left( x \right) = \sin^2 x\] and the composite function \[g\left( f\left( x \right) \right) = \left| \sin x \right|\] then g(x) is equal to
Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
Write about strcmp() function.
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Which of the following functions from Z into Z are bijections?
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever
Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Three friends F1, F2, and F3 exercised their voting right in general election-2019, then which of the following is true?
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- The function f: R → R defined by f(x) = x − 4 is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
If f: R→R is a function defined by f(x) = `[x - 1]cos((2x - 1)/2)π`, where [ ] denotes the greatest integer function, then f is ______.
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
