Advertisements
Advertisements
प्रश्न
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
उत्तर
R = {(a, b): a, b ∈ Z, a – b is an integer}
If a, b ∈ Z, then a - b ∈ Z
=> Every ordered pair of integers is contained in R.
R ={(a, b) : a, b ∈ Z}
So, Range of R = Domain of R = Z.
संबंधित प्रश्न
Let A = {1, 2, 3, …, 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
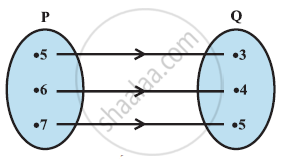
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a, b ∈ A, b is exactly divisible by a}.
- Write R in roster form
- Find the domain of R
- Find the range of R.
Find the inverse relation R−1 in each of the cases:
(ii) R = {(x, y), : x, y ∈ N, x + 2y = 8}
Let A = [1, 2, 3, 4, 5, 6]. Let R be a relation on A defined by {(a, b) : a, b ∈ A, b is exactly divisible by a}
(i) Writer R in roster form
(ii) Find the domain of R
(ii) Find the range of R.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(i) (a, b) R (a, b) for all (a, b) ∈ N × N
If A = {1, 2, 4}, B = {2, 4, 5} and C = {2, 5}, write (A − C) × (B − C).
If A = [1, 3, 5] and B = [2, 4], list of elements of R, if
R = {(x, y) : x, y ∈ A × B and x > y}
If A = [1, 2, 3], B = [1, 4, 6, 9] and R is a relation from A to B defined by 'x' is greater than y. The range of R is
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation on Z, then the domain of R is ______.
A relation ϕ from C to R is defined by x ϕ y ⇔ |x| = y. Which one is correct?
R is a relation from [11, 12, 13] to [8, 10, 12] defined by y = x − 3. Then, R−1 is
If the set A has p elements, B has q elements, then the number of elements in A × B is
Let R be a relation from a set A to a set B, then
Let A = {1, 2, 3, 4), B = {4, 5, 6}, C = {5, 6}. Verify, A × (B ∩ C) = (A × B) ∩ (A × C)
Select the correct answer from given alternative.
A relation between A and B is
Select the correct answer from given alternative
If A = {a, b, c} The total no. of distinct relations in A × A is
Answer the following:
If A = {1, 2, 3}, B = {4, 5, 6} check if the following are relations from A to B. Also write its domain and range
R3 = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/a ∈ N, a < 5, b = 4}
Answer the following:
R = {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} Check if R is symmentric
Answer the following:
Show that the following is an equivalence relation
R in A is set of all books. given by R = {(x, y)/x and y have same number of pages}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R1 = {(2, 1), (7, 1)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R3 = {(2, –1), (7, 7), (1, 3)}
Let A = {1, 2, 3, 4, …, 45} and R be the relation defined as “is square of ” on A. Write R as a subset of A × A. Also, find the domain and range of R
A Relation R is given by the set `{(x, y)/y = x + 3, x ∈ {0, 1, 2, 3, 4, 5}}`. Determine its domain and range
A company has four categories of employees given by Assistants (A), Clerks (C), Managers (M), and an Executive Officer (E). The company provides ₹ 10,000, ₹ 25,000, ₹ 50,000, and ₹ 1,00,000 as salaries to the people who work in the categories A, C, M, and E respectively. If A1, A2, A3, A4, and A5 were Assistants; C1, C2, C3, C4 were Clerks; M1, M2, M3 were managers and E1, E2 was Executive officers and if the relation R is defined by xRy, where x is the salary given to person y, express the relation R through an ordered pair and an arrow diagram
Multiple Choice Question :
Let n(A) = m and n(B) = n then the total number of non-empty relation that can be defined from A to B is ________.
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence
Let P be the set of all triangles in a plane and R be the relation defined on P as aRb if a is similar to b. Prove that R is an equivalence relation
Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is transitive
Choose the correct alternative:
Let R be the universal relation on a set X with more than one element. Then R is
Is the given relation a function? Give reasons for your answer.
s = {(n, n2) | n is a positive integer}
Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is ______.
Let S = {x ∈ R : x ≥ 0 and `2|sqrt(x) - 3| + sqrt(x)(sqrt(x) - 6) + 6 = 0}`. Then S ______.
Let N denote the set of all natural numbers. Define two binary relations on N as R1 = {(x, y) ∈ N × N : 2x + y = 10} and R2 = {(x, y) ∈ N × N : x + 2y = 10}. Then ______.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a function from A to B
Justify your answer in case.
