Advertisements
Advertisements
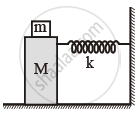
प्रश्न
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Advertisements
उत्तर १
(a) x = 2sin 20t
(b) x = 2cos 20t
(c) x = –2cos 20t
The functions have the same frequency and amplitude, but different initial phases.
Distance travelled by the mass sideways, A = 2.0 cm
Force constant of the spring, k = 1200 N m–1
Mass, m = 3 kg
Angular frequency of oscillation:
`omega = sqrt(k/m)`
`= sqrt(1200/3)= sqrt400 = 20 rad s^(-1)`
a) When the mass is at the mean position, initial phase is 0.
Displacement, x = Asin ωt
= 2sin 20t
b) At the maximum stretched position, the mass is toward the extreme right. Hence, the initial phase is `pi/2`
Displacement , `x = Asin(omegat + pi/2)`
`= 2sin (20t + pi/2)`
= 2cos 20t
(c) At the maximum compressed position, the mass is toward the extreme left. Hence, the initial phase is `(3pi)/2`
Displacement, `x = Asin(omegat + 3pi/2)`
`= 2sin (20t + 3pi/2) = - 2 cos 20 t`
The functions have the same frequency (`20/(2pi) Hz`) and amplitude (2 cm), but different initial phases `(0, pi/2, (3pi)/2)`
उत्तर २
a =2 cm, omega = `sqrt(k/m) = sqrt(1200/3) s^(-1)= 20s^(-1)`
a) Since time s measured from mean position
b) At the maximum stretched position, tyhe body is at the extreme right position. The initial phase is `pi/2`
`:. x = a sin (omegat + pi/2) = a cos omegat = 2 cos 20 t`
c) At the maximum compressed position, the body is at the extreme left position. The initial phase is `(3pi)/2`
`:. x = a sin (omegat + (3pi)/2) = - a cosomegat = - 2 cos 20t`
APPEARS IN
संबंधित प्रश्न
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
