Advertisements
Advertisements
प्रश्न
Multiple Choice Question. Select the correct option.
A force acts on a body of mass 3 kg such that its velocity changes from 4 ms−1 to 10 ms−1. The change in momentum of the body is
विकल्प
42 kgms−1
2 kgms−1
18 kgms−1
14 kgms−1
उत्तर
18 kgms−1
Explanation:
Mass = m = 3 kg
Velocity v1 = 4 ms−1
Velocity = v2 = 10 ms−1
Change in momentum of body
= mv2 – mv1 = m (v2 – v1) = 3 (10 – 4)
= 3 × 6 =18 kgms−1
APPEARS IN
संबंधित प्रश्न
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
Find the acceleration of the 500 g block in the following figure.
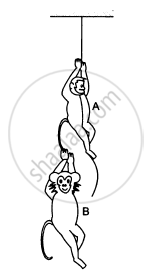
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
Use Newton's second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
A car is moving with a uniform velocity 30 ms-1. It is stopped in 2 s by applying a force of 1500 N through its brakes. Calculate the following values : The change in momentum of car.
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
How long will a stone take to fall to the ground from the top of a building 80 m high
An electron of mass 9 × 10−31 kg is moving with a linear velocity of 6 × 107 ms−1. Calculate the linear momentum of electron.
Define Newton’s second law of motion.
