Advertisements
Advertisements
प्रश्न
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
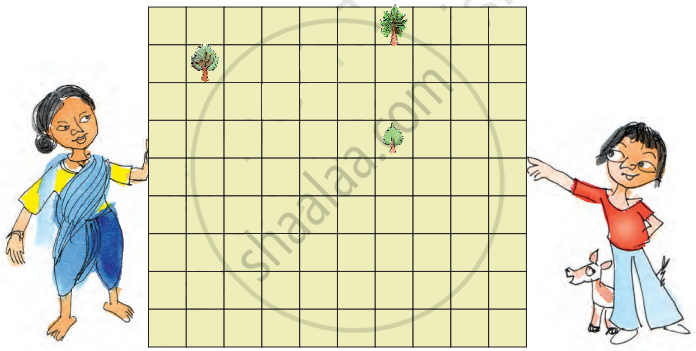
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
उत्तर
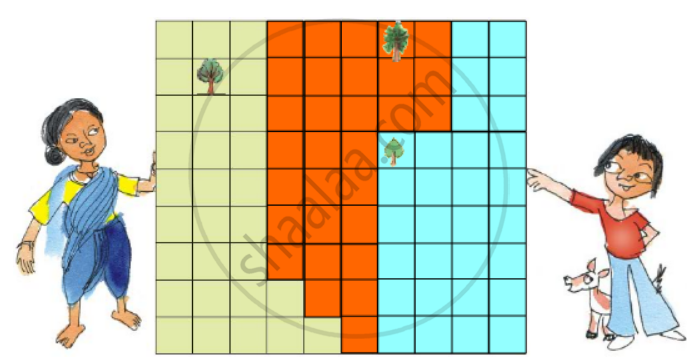
Total number of boxes = 90
Hence, one person’s share
= 90/3 = 30
The division can be done as the given figure.
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

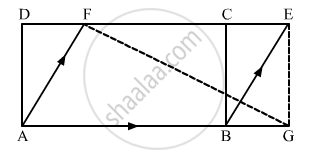
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
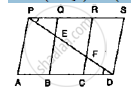
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Find the area of a rectangle whose length = 15 cm breadth = 6.4 cm
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Which has the bigger area - one of your footprints or the page of this book?
Which has the smaller area - two five-rupee notes together or a hundred rupee notes?
Is the area of your belt the same as the area of the postcard? Why or why not?
Look at the table. If you were to write the area of each of these which column would you choose? Make a (✓).
| Square cm |
Square meter |
Square km |
|
| Handkerchief | ✓ | ||
| Sari | |||
| Page of your book | |||
| School land | |||
| Total land of a city | |||
| Door of your classroom | |||
| Chair seat | |||
| Blackboard | |||
| Indian flag | |||
| Land over which a river flows |
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What is its area? Is it more than the first rectangle?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 50 boxes. There are 48 fruits in one box.
Tick the one question which matches with the given problem.
Explain why (a) and (c) are not good choices.a) How much will the shopkeeper pay in all? b) How many fruits are there in all? ✓ c) How many more boxes will he need?
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:
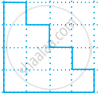
Find the area of the following figure by counting squares:

