Advertisements
Advertisements
प्रश्न
निम्न समस्या में रैखिक समीकरण के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए।
5 पेंसिल तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य ₹ 46 है। एक पेंसिल का मूल्य तथा एक कलम मूल्य ज्ञात कीजिए।
उत्तर
माना एक पेन्सिल मूल्य = x रू.
और एक कलम का मूल्य = y रू.
प्रश्नानुसार,
5x + 7y = 50 ...(1) और
7x + 5y = 46 ...(2)
समी. (1) से
5x + 7y = 50
⇒ 5x = 50 - 7y
⇒ x = `(50 - 7y)/5`
| x | 3 | 10 | -4 |
| y | 5 | 0 | 10 |
समी. (2) से
7x + 5y = 46
⇒ 7x = 46 - 5y
⇒ x = `(46 - 5y)/7`
| x | 8 | 3 | -2 |
| y | -2 | 5 | 12 |
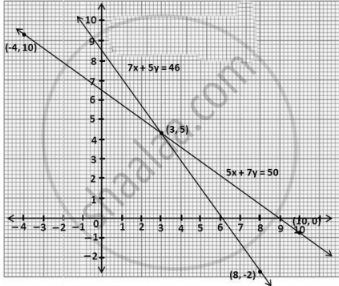
ग्राफीय विधि से हल के लिए हम जब बने ग्राफ को देखते हैं तो पाते हैं कि बिंदु (3, 5) दिए गए समीकरण के लिए प्रतिच्छेदन बिंदु है जो कि रैखिक समीकरण युग्म का उभयनिष्ठ हल है।
इसलिए, पेन्सिल का मूल्य = 3 और कलम का मूल्य = 5 है।
APPEARS IN
संबंधित प्रश्न
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
3x + 2y = 5; 2x - 3y = 7
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
2x - 3y = 8; 4x - 6y = 9
निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए।
x - y = 8, 3x - 3y = 16
समीकरणों 5x - y = 5 और 3x - y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
क्या समीकरणों के निम्नलिखित युग्म का कोई हल नहीं है? अपने उत्तर का औचित्य दीजिए।
x = 2y, y = 2x
क्या रैखिक समीकरणों के निम्नलिखित युग्म संगत हैं? अपने उत्तरों का औचित्य दीजिए।
2ax + by = a, 4ax + 2by – 2a = 0; a, b ≠ 0
समीकरण λx + 3y = –7, 2x + 6y = 14 के युग्म के अपरिमित रूप से अनेक हल होने के लिए, λ का मान 1 होना चाहिए। क्या यह कथन सत्य है? कारण दीजिए।
आलेखीय विधि से ज्ञात कीजिए कि निम्नलिखित समीकरण युग्म संगत हैं या नहीं। यदि संगत हैं, तो इन्हें हल कीजिए।
x + y = 3, 3x + 3y = 9
रेखाओं y = x, 3y = x और x + y = 8 से बनने वाले त्रिभुज के शीर्षों के निर्देशांक आलेखीय विधि से निर्धारित कीजिए।
समीकरण x = 3, x = 5 और 2x – y – 4 = 0 के आलेख खींचिए। इन रेखाओं और x-अक्ष द्वारा बनाए गए चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
