Advertisements
Advertisements
प्रश्न
निम्नलिखित की रचना कीजिए और रचना का औचित्य दीजिए -
एक समकोण त्रिभुज जिसकी एक भुजा 3.5 cm तथा अन्य भुजा और कर्ण का योग 5.5 cm है।
उत्तर
समकोण त्रिभुज ABC में, दिया है BC = 3.5 सेमी, ∠B = 90° और दूसरी भुजा और कर्ण का योग है, AB + AC = 5.5 सेमी
एक त्रिभुज ABC बनाने के लिए निम्नलिखित चरणों का उपयोग करें -
1. आधार BC = 3.5 सेमी खींचिए।
2. आधार BC के बिंदु B पर एक कोण XBC = 90° बनाएं।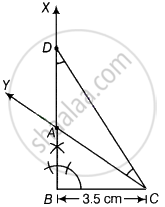
3. रेखा खंड BD को AB + AC के बराबर काटें, यानी किरण XB से 5.5 सेमी।
4. DC को मिलाइए और ∠DCY को ∠BDC के बराबर कीजिए।
5. माना Y, BX को A पर प्रतिच्छेद करता है। इसलिए, ABC अभीष्ट त्रिभुज है।
औचित्य -
आधार BC और ∠B दिए गए अनुसार बनाए गए हैं।
∠ACD में, ∠ACD = ∠ADC ...[रचना द्वारा]
AD = AC ...(i) [समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
अब, AB = BD – AD = BD – AC ...[समीकरण (i) से]
BD = AB + AC
इसलिए, हमारी रचना उचित है।
APPEARS IN
संबंधित प्रश्न
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 सेमी, ∠B = 75° और AB + AC = 13 सेमी हो।
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 सेमी, ∠B = 45° और AB – AC = 3.5 सेमी हो।
एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 सेमी, ∠Q = 60° और PR – PQ = 2 सेमी हो।
एक त्रिभुज XYZ की रचना कीजिए, जिसमें ∠Y = 30°, ∠Z = 90° और XY + YZ + ZX = 11 सेमी हो।
एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 सेमी और कर्ण तथा अन्य भुजा का योग 18 सेमी है।
एक त्रिभुज ABC, जिसमें BC = 6 cm और ∠B = 45° दिया है, की रचना संभव नहीं है, यदि AB और AC का अंतर है :
3.6 cm, 3.0 cm और 4.8 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए। सबसे छोटे कोण को समद्विभाजित कीजिए तथा प्रत्येक भाग को मापिए।
निम्नलिखित की रचना कीजिए और रचना का औचित्य दीजिए -
एक त्रिभुज, यदि उसका परिमाप 10.4 cm और दो कोण 45° और 120° हैं।
निम्नलिखित की रचना कीजिए और रचना का औचित्य दीजिए -
एक त्रिभुज PQR, जबकि QR = 3 cm, ∠PQR = 45° और QP – PR = 2 cm दिया है।
निम्नलिखित की रचना कीजिए और रचना का औचित्य दीजिए -
एक समबाहु त्रिभुज, यदि इसका शीर्षलंब 3.2 cm है।
