Advertisements
Advertisements
प्रश्न
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
- What do you call the point O?
- What is the relation between the distances OA, OB and OC?
- Does the perpendicular bisector of BC pass through O?
उत्तर
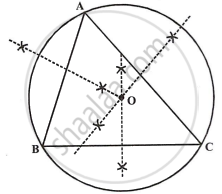
- O is called the circumcentre of circumcircle of ΔABC.
- OA, OB and OC are the radii of the circumcircle.
- Yes, the perpendicular bisector of BC will pass through O.
APPEARS IN
संबंधित प्रश्न
Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5
cm and ∠ABC = 120°
1) Construct a circum-circle of ΔABC
2) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Construct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Using a ruler and compasses only:
- Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
- In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
- Measure ∠BCP.
Draw a circle of radius 2. 5 cm and circumscribe a square about it.
Draw a line segment OA , 5 cm long. AT O , using ruler and compasses only, construct OB such that , ∠ AOB = 37.5° construct a circle to touch OA at A and to touch OB at B.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
Construct a triangle whose sides are 4.4 cm, 5.2 cm, and 7.1 cm. Construct its circumcircle. Write also the steps of construction.
Use ruler and compasses only for this question:
(i) Construct A ABC, where AB = 3.5 cm, BC = 6 cm and ∠ ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC, and also equidistant from B and C. Measure and record the length of PB.
Construct a ΔABC with base BC = 3.5 cm, vertical angle ∠ BAC = 45°, and median through the vertex A is 3.5 cm. Write also the steps of construction.
(i) Construct a triangle ABC, in which AB = 5.0 cm, BC = 3.5 cm and ∠ ABC = `67 1/2°`
( Use a pair of compasses and ruler only.)
(ii) Construct a circle to touch AB at B and it pass though C.
