Advertisements
Advertisements
प्रश्न
Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.
उत्तर
Let us assume that in a closed equipotential surface with no charge the potential is changing from position to position. Let the potential just inside the surface is different to that of the surface causing a potential gradient (dV/dr)
It means E ≠ 0 electric field comes into existence, which is given by as E = – dV/dr
It means there will be field lines pointing inwards or outwards from the surface. These lines cannot be again on the surface, as the surface is equipotential. It is possible only when the other end of the field lines originated from the charges inside. This contradicts the original assumption. Hence, the entire volume inside must be equipotential.
APPEARS IN
संबंधित प्रश्न
The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
What is the geometrical shape of equipotential surfaces due to a single isolated charge?
Define equipotential surface.
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Find the amount of work done in rotating an electric dipole of dipole moment 3.2 x 10- 8Cm from its position of stable equilibrium to the position of unstable equilibrium in a uniform electric field if intensity 104 N/C.
The diagrams below show regions of equipotentials.
(i) |
(ii)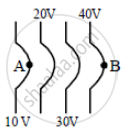 |
(iii) |
(iv) |
A positive charge is moved from A to B in each diagram.
- The potential at all the points on an equipotential surface is same.
- Equipotential surfaces never intersect each other.
- Work done in moving a charge from one point to other on an equipotential surface is zero.
The work done to move a charge along an equipotential from A to B ______.
- cannot be defined as `- int_A^B E.dl`
- must be defined as `- int_A^B E.dl`
- is zero.
- can have a non-zero value.
What is meant by an equipotential surface?
