Advertisements
Advertisements
प्रश्न
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
उत्तर
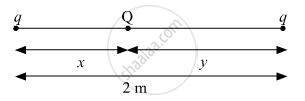
`(K(q)(Q))/x = (-K(q)(q))/2`
⇒ `Q = (-qx)/2`
`because (KqQ)/x = (KQq)/y`
x = y
x + y = 2
∴ x = y = 1
`Q = (-q)/2`
संबंधित प्रश्न
Two charges 2 μC and −2 µC are placed at points A and B 6 cm apart.
- Identify an equipotential surface of the system.
- What is the direction of the electric field at every point on this surface?
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning?
(Hint: The earth has an electric field of about 100 Vm−1 at its surface in the downward direction, corresponding to a surface charge density = −10−9 C m−2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Why is there no work done in moving a charge from one point to another on an equipotential surface?
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Find the amount of work done in rotating an electric dipole of dipole moment 3.2 x 10- 8Cm from its position of stable equilibrium to the position of unstable equilibrium in a uniform electric field if intensity 104 N/C.
Statement - 1: For practical purpose, the earth is used as a reference at zero potential in electrical circuits.
Statement - 2: The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by `Q/(4piepsilon_0R)`.
Assertion: Electric field is discontinuous across the surface of a spherical charged shell.
Reason: Electric potential is continuous across the surface of a spherical charged shell.
Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately.
Can two equipotential surfaces intersect each other?
