Advertisements
Advertisements
प्रश्न
Find the amount of work done in rotating an electric dipole of dipole moment 3.2 x 10- 8Cm from its position of stable equilibrium to the position of unstable equilibrium in a uniform electric field if intensity 104 N/C.
उत्तर
Given: p = 3.2 x 10- 8Cm, E = 104 N/C
To Find: Work done in rotating dipole (W)
Formula: W = pE (cos θ0 - cos θ)
Calculation:
At stable equilibrium, θ0 = 0°
At unstable equilibrium, θ = 180°
From formula,
W = pE (cos θ0 - cos θ)
= 3.2 × 10-8 × 104 (cos 0 - cos 180)
= 3.2 × 10-4 [1 - (-1)]
= 6.4 × 10-4 J
Work done in rotating an electric dipole is 6.4 × 10-4 J.
APPEARS IN
संबंधित प्रश्न
Define an equipotential surface.
Draw a sketch of equipotential surfaces due to a single charge (-q), depicting the electric field lines due to the charge
A regular hexagon of side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning?
(Hint: The earth has an electric field of about 100 Vm−1 at its surface in the downward direction, corresponding to a surface charge density = −10−9 C m−2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Why is there no work done in moving a charge from one point to another on an equipotential surface?
Depict the equipotential surfaces for a system of two identical positive point charges placed a distance(d) apart?
Draw the equipotential surfaces due to an electric dipole.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Answer the following question.
Write two important characteristics of equipotential surfaces.
Statement - 1: For practical purpose, the earth is used as a reference at zero potential in electrical circuits.
Statement - 2: The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by `Q/(4piepsilon_0R)`.
A particle of mass 'm' having charge 'q' is held at rest in uniform electric field of intensity 'E'. When it is released, the kinetic energy attained by it after covering a distance 'y' will be ______.
The diagrams below show regions of equipotentials.
(i) |
(ii)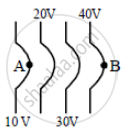 |
(iii) |
(iv) |
A positive charge is moved from A to B in each diagram.
Equipotential surfaces ______.
Which of the following is NOT the property of equipotential surface?
Can two equipotential surfaces intersect each other?
Consider a uniform electric field in the ẑ direction. The potential is a constant ______.
- in all space.
- for any x for a given z.
- for any y for a given z.
- on the x-y plane for a given z.
Equipotential surfaces ______.
- are closer in regions of large electric fields compared to regions of lower electric fields.
- will be more crowded near sharp edges of a conductor.
- will be more crowded near regions of large charge densities.
- will always be equally spaced.
What is meant by an equipotential surface?
