Advertisements
Advertisements
प्रश्न
Find the amount of work done in rotating an electric dipole of dipole moment 3.2 x 10- 8Cm from its position of stable equilibrium to the position of unstable equilibrium in a uniform electric field if intensity 104 N/C.
उत्तर
Given: p = 3.2 x 10- 8Cm, E = 104 N/C
To Find: Work done in rotating dipole (W)
Formula: W = pE (cos θ0 - cos θ)
Calculation:
At stable equilibrium, θ0 = 0°
At unstable equilibrium, θ = 180°
From formula,
W = pE (cos θ0 - cos θ)
= 3.2 × 10-8 × 104 (cos 0 - cos 180)
= 3.2 × 10-4 [1 - (-1)]
= 6.4 × 10-4 J
Work done in rotating an electric dipole is 6.4 × 10-4 J.
APPEARS IN
संबंधित प्रश्न
Draw a sketch of equipotential surfaces due to a single charge (-q), depicting the electric field lines due to the charge
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm−1. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside!)
A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m2. Will he get an electric shock if he touches the metal sheet next morning?
The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning?
(Hint: The earth has an electric field of about 100 Vm−1 at its surface in the downward direction, corresponding to a surface charge density = −10−9 C m−2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Draw equipotential surfaces:
(1) in the case of a single point charge and
(2) in a constant electric field in Z-direction. Why are the equipotential surfaces about a single charge not equidistant?
(3) Can electric field exist tangential to an equipotential surface? Give reason
What is the geometrical shape of equipotential surfaces due to a single isolated charge?
Depict the equipotential surfaces for a system of two identical positive point charges placed a distance(d) apart?
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Statement - 1: For practical purpose, the earth is used as a reference at zero potential in electrical circuits.
Statement - 2: The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by `Q/(4piepsilon_0R)`.
A particle of mass 'm' having charge 'q' is held at rest in uniform electric field of intensity 'E'. When it is released, the kinetic energy attained by it after covering a distance 'y' will be ______.
Assertion: Electric field is discontinuous across the surface of a spherical charged shell.
Reason: Electric potential is continuous across the surface of a spherical charged shell.
Consider the following statements and select the correct statement(s).
- Electric field lines are always perpendicular to equipotential surface.
- No two equipotential surfaces can intersect each other.
- Electric field lines are in the direction of tangent to an equipotential surface.
Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately.
The diagrams below show regions of equipotentials.
(i) |
(ii)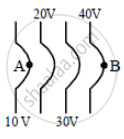 |
(iii) |
(iv) |
A positive charge is moved from A to B in each diagram.
- The potential at all the points on an equipotential surface is same.
- Equipotential surfaces never intersect each other.
- Work done in moving a charge from one point to other on an equipotential surface is zero.
Equipotential surfaces ______.
Equipotential surfaces ______.
- are closer in regions of large electric fields compared to regions of lower electric fields.
- will be more crowded near sharp edges of a conductor.
- will be more crowded near regions of large charge densities.
- will always be equally spaced.
The work done to move a charge along an equipotential from A to B ______.
- cannot be defined as `- int_A^B E.dl`
- must be defined as `- int_A^B E.dl`
- is zero.
- can have a non-zero value.
Draw equipotential surfaces for (i) an electric dipole and (ii) two identical positive charges placed near each other.
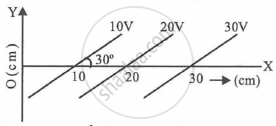
Equipotential surfaces are shown in figure. Then the electric field strength will be ______.