Advertisements
Advertisements
प्रश्न
The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm−1. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside!)
उत्तर
We do not get an electric shock as we step out of our house because the original equipotential surfaces of open-air change, keeping our body and the ground at the same potential.
APPEARS IN
संबंधित प्रश्न
Define an equipotential surface.
Two charges 2 μC and −2 µC are placed at points A and B 6 cm apart.
- Identify an equipotential surface of the system.
- What is the direction of the electric field at every point on this surface?
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Why is there no work done in moving a charge from one point to another on an equipotential surface?
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Answer the following question.
Write two important characteristics of equipotential surfaces.
Assertion: Electric field is discontinuous across the surface of a spherical charged shell.
Reason: Electric potential is continuous across the surface of a spherical charged shell.
Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately.
Consider a uniform electric field in the ẑ direction. The potential is a constant ______.
- in all space.
- for any x for a given z.
- for any y for a given z.
- on the x-y plane for a given z.
The work done to move a charge along an equipotential from A to B ______.
- cannot be defined as `- int_A^B E.dl`
- must be defined as `- int_A^B E.dl`
- is zero.
- can have a non-zero value.
Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.
Find the equation of the equipotentials for an infinite cylinder of radius r0, carrying charge of linear density λ.
Draw equipotential surfaces for (i) an electric dipole and (ii) two identical positive charges placed near each other.
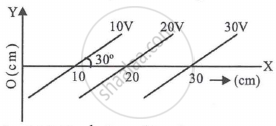
Equipotential surfaces are shown in figure. Then the electric field strength will be ______.