Advertisements
Advertisements
प्रश्न
The work done to move a charge along an equipotential from A to B ______.
- cannot be defined as `- int_A^B E.dl`
- must be defined as `- int_A^B E.dl`
- is zero.
- can have a non-zero value.
विकल्प
a and b
b and c
c and d
a and c
उत्तर
b and c
Explanation:
The work done by the external agent in shifting the test charge along the dashed line from 1 to 2 is
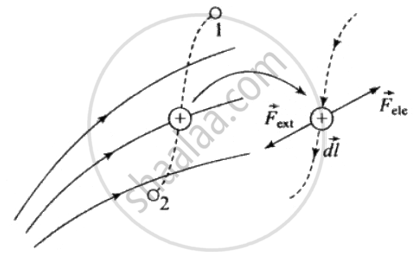
|
The external agent does a work `W = - q int_1^2 vecE * vec(dl)` in transporting the test charge q slowly from the positions 1 to 2 in the static electric field. |
`W_("ext") = int_1^2 vecF_("ext") * vec(dl) int_1^2 (-qvecE) * vec(dl) = - q int_1^2 vecE * vec(dl)`
We know `V_A - V_B = - int_A^B vecE * vec(dl)` ......(i)
`W_("electrical") = -ΔU = - qΔV = q(V_A - V_B)` ......(ii)
Hence from (i) and (ii), `W_("electrical") = q(V_A - V_B) = - qint_A^B vecE * vec(dl)`
If we want to calculate the work done to move a charge along an equipotential from A to B
For equipotential surface VA = VB, hence W = 0
Also electric field is perpendicular to equipotential surface, hence `vecE * vec(dl) => W_("electrical") = 0`
APPEARS IN
संबंधित प्रश्न
Draw a sketch of equipotential surfaces due to a single charge (-q), depicting the electric field lines due to the charge
Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Define equipotential surface.
Answer the following question.
Two identical point charges, q each, are kept 2m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
The diagrams below show regions of equipotentials.
(i) |
(ii)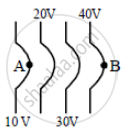 |
(iii) |
(iv) |
A positive charge is moved from A to B in each diagram.
- The potential at all the points on an equipotential surface is same.
- Equipotential surfaces never intersect each other.
- Work done in moving a charge from one point to other on an equipotential surface is zero.
Equipotential surfaces ______.
- are closer in regions of large electric fields compared to regions of lower electric fields.
- will be more crowded near sharp edges of a conductor.
- will be more crowded near regions of large charge densities.
- will always be equally spaced.
Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.
