Advertisements
Advertisements
प्रश्न
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
उत्तर
L.H.S.
= `(tan(90° - θ)cotθ)/("cosec"^2 θ)`
= `(cotθ xx cotθ)/("cosec^2 θ)`
= `(cot^2 θ)/("cosec"^2 θ)`
= `((cos^2 θ)/(sin^2 θ))/((1)/(sin^2 θ)`
= cos2θ
= R.H.S.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if sec 2A = 2
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Solve for x : 3 tan2 (2x - 20°) = 1
Find the value of 'A', if (2 - cosec 2A) cos 3A = 0
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
Find the value 'x', if: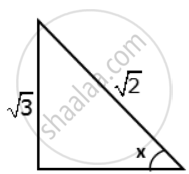
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.
In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:
a. the height of the rocket when it is at point R.
b. the horizontal distance of point S from P.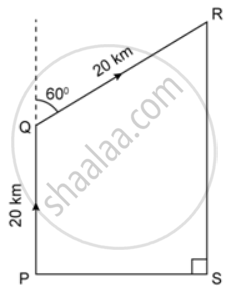
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
