Advertisements
Advertisements
प्रश्न
Solve for x : 3 tan2 (2x - 20°) = 1
उत्तर
3 tan2 ( 2x – 20°) = 1
tan ( 2x – 20°) = `(1)/(sqrt3)`
tan ( 2x – 20°) = tan 30°
2x –20° = 30°
2x = 50°
x = 25°
APPEARS IN
संबंधित प्रश्न
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Solve for x : cos2 30° + sin2 2x = 1
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ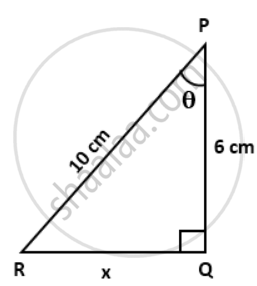
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB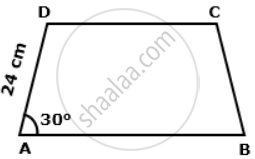
Find the value 'x', if: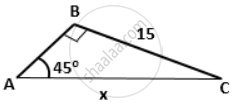
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
