Advertisements
Advertisements
प्रश्न
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB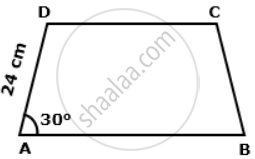
उत्तर
Construction: Draw DP ⊥ AB and CM ⊥ AB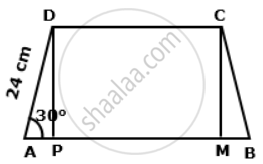
a. In right ΔADP,
cos30° = `"AP"/"AD"`
⇒ `sqrt(3)/(2) = "AP"/(24)`
⇒ AP = `12sqrt(13)"cm"`
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
b. In right ΔADP,
sin30° = `"PD"/"AD"`
⇒ `(1)/(2) = "PD"/(24)`
⇒ PD = 12cm
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
Calculate the value of A, if (tan A - 1) (cosec 3A - 1) = 0
Solve for x : cos `(x)/(3) –1` = 0
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
In a rectangle ABCD, AB = 20cm, ∠BAC = 60°, calculate side BC and diagonals AC and BD.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE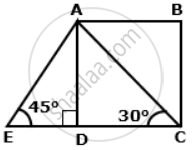
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
