Advertisements
Advertisements
प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
विकल्प
Increases
Decreases
उत्तर
For acute angles, remember what sine means: opposite over hypotenuse. If we increase the angle, then the opposite side gets larger. That means "opposite/hypotenuse" gets larger or increases.
APPEARS IN
संबंधित प्रश्न
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
If θ < 90°, find the value of: `tan^2θ - (1)/cos^2θ`
In the given figure, if tan θ = `(5)/(13), tan α = (3)/(5)` and RS = 12m, find the value of 'h'.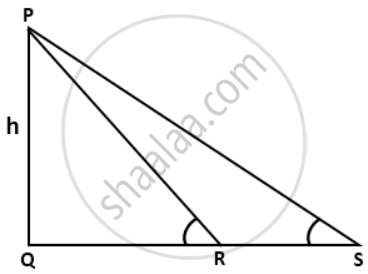
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Evaluate the following: sec16° tan28° - cot62° cosec74°
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`
If cosθ = sin60° and θ is an acute angle find the value of 1- 2 sin2θ
