Advertisements
Advertisements
प्रश्न
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
योग
उत्तर
sec2θ = cosec3θ
⇒ sec2θ = sec(90° - 3θ)
⇒ 2θ = 90° - 3θ
⇒ 5θ = 90°
⇒ θ = 18°.
shaalaa.com
Trigonometric Equation Problem and Solution
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
APPEARS IN
संबंधित प्रश्न
Solve for x : 2 cos 3x - 1 = 0
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
Find:
a. BC
b. AD
c. AC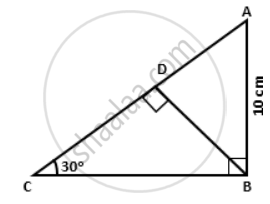
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.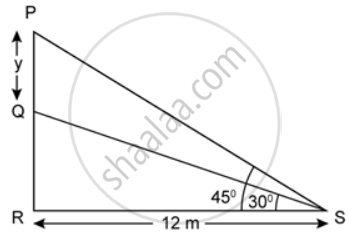
Evaluate the following: `(tan12°)/(cot78°)`
Evaluate the following: cosec 54° - sec 36°
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
If cosθ = sin60° and θ is an acute angle find the value of 1- 2 sin2θ
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
