Advertisements
Advertisements
प्रश्न
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
उत्तर
sec2θ = cosec3θ
⇒ sec2θ = sec(90° - 3θ)
⇒ 2θ = 90° - 3θ
⇒ 5θ = 90°
⇒ θ = 18°.
APPEARS IN
संबंधित प्रश्न
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.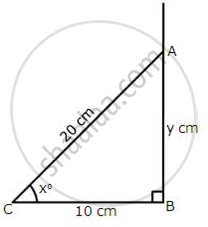
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Find the value of 'A', if 2 sin 2A = 1
If tanθ= cotθ and 0°≤ θ ≤ 90°, find the value of 'θ'.
Find the length of EC.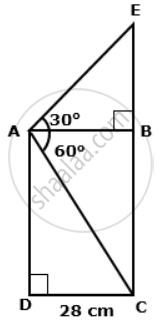
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin65° + cot59°
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
If A + B = 90°, prove that `(tan"A" tan"B" + tan"A" cot"B")/(sin"A" sec"B") - (sin^2"B")/(cos^2"A")` = tan2A
