Advertisements
Advertisements
Question
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB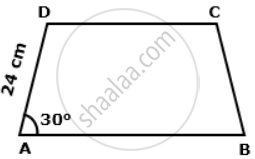
Solution
Construction: Draw DP ⊥ AB and CM ⊥ AB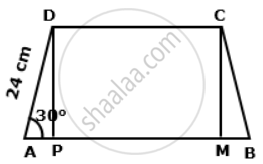
a. In right ΔADP,
cos30° = `"AP"/"AD"`
⇒ `sqrt(3)/(2) = "AP"/(24)`
⇒ AP = `12sqrt(13)"cm"`
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
b. In right ΔADP,
sin30° = `"PD"/"AD"`
⇒ `(1)/(2) = "PD"/(24)`
⇒ PD = 12cm
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
APPEARS IN
RELATED QUESTIONS
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Solve the following equation for A, if tan 3 A = 1
Solve for x : 3 tan2 (2x - 20°) = 1
If θ = 30°, verify that: tan2θ = `(2tanθ)/(1 - tan^2θ)`
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
