Evaluate the following: 2 sin 28 ° cos 62 ° + 3 cot 49 ° tan 41 ° - Mathematics

Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`

Sum

`(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`

= `(2sin(90° - 62°))/(cos62°) + (3cot(90° - 41°))/(tan41°)`

= `(2cos62°)/(cos62°) + (3tan41°)/(tan41°)`

= 2 + 3
= 5.

shaalaa.com

Trigonometric Equation Problem and Solution

Is there an error in this question or solution?

Chapter 27: Trigonometrical Ratios of Standard Angles - Exercise 27.3

Chapter 27 Trigonometrical Ratios of Standard Angles
Exercise 27.3 | Q 3.3

Use the given figure to find:
(i) tanθ°
(ii) θ°
(iii) sin²θ° - cos²θ°(iv) Use sin θ° to find the value of x.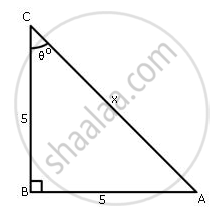

Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0

If 3 tan A - 5 cos B = `sqrt3` and B = 90°, find the value of A

Find the value of 'A', if 2 cos A = 1

Solve for 'θ': `sin θ/(3)` = 1

If tanθ= cotθ and 0°≤ θ ≤ 90°, find the value of 'θ'.

If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°

If θ < 90°, find the value of: sin²θ + cos²θ

Find x and y, in each of the following figure: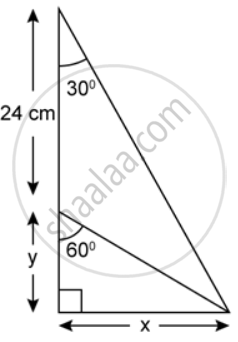

If A + B = 90°, prove that `(tan"A" tan"B" + tan"A" cot"B")/(sin"A" sec"B") - (sin^2"B")/(cos^2"A")` = tan²A