Advertisements
Advertisements
Question
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Solution
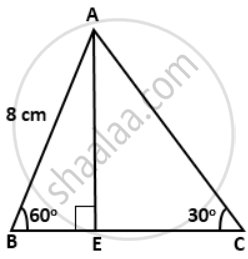
a. In right ΔAEB,
sin60° = `"AE"/"AB"`
⇒ `sqrt(3)/(2) = "AE"/(8)`
⇒ AE = `4sqrt(3)"cm"`
Now,
BE2
= AB2 - AE2
= `8^2 - (4sqrt(3))^2`
= 64 - 48
= 16
⇒ BE = 4cm
b. EC
= BC - BE
= 24 - 4
= 20cm
Now,
In right ΔAEC,
AC2
= AE2 + EC2
= `(4sqrt(3))^2 + 20^2`
= 48 + 400
= 448
⇒ AC = `8sqrt(7)"cm"`.
APPEARS IN
RELATED QUESTIONS
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
Solve for x : sin2 x + sin2 30° = 1
Find the value of 'A', if `sqrt(3)cot"A"` = 1
Solve for 'θ': cot2(θ - 5)° = 3
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.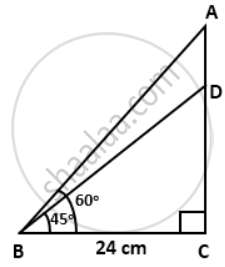
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB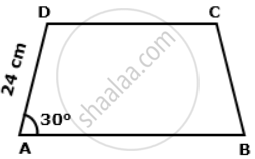
Find the value 'x', if:
Find the value 'x', if:
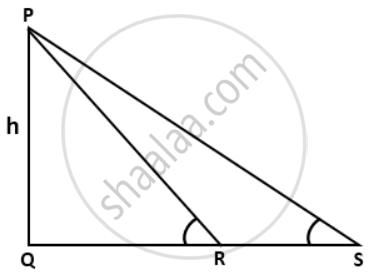
In the given figure, if tan θ = `(5)/(13), tan α = (3)/(5)` and RS = 12m, find the value of 'h'.