Advertisements
Advertisements
Question
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE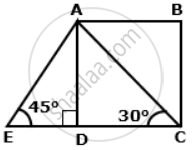
Solution

a. In right ΔADC,
tan30° = `"AD"/"DC"`
⇒ `(1)/sqrt(3) = (1.5)/"DC"`
⇒ DC = `1.5sqrt(3)`
Since AB || DC and AD ⊥ EC, ABCD is a parallelogram and hence opposite sides are equal.
⇒ AB
= DC
= `1.5sqrt(3)"cm"`.
b. In right ΔADC,
sin30° = `"AD"/"AC"`
⇒ `(1)/(2) = (1.5)/"AC"`
⇒ AC
= 2 x 1.5
= 3cm.
c. In right ΔADE,
sin45° = `"AD"/"AE"`
⇒ `(1)/sqrt(2) = (1.5)/"AE"`
⇒ AE = `1.5sqrt(2)`.
APPEARS IN
RELATED QUESTIONS
If sin x + cos y = 1 and x = 30°, find the value of y
Solve the following equation for A, if 2 sin 3 A = 1
Solve for x : cos (2x - 30°) = 0
Solve for x : cos2 30° + sin2 2x = 1
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.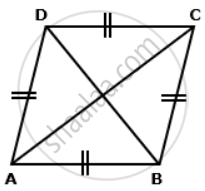
Find the length of EC.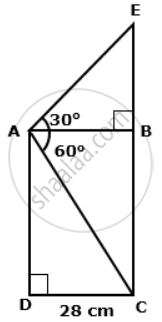
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Find the value 'x', if: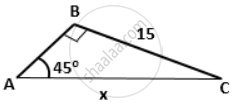
If tan x° = `(5)/(12) . tan y° = (3)/(4)` and AB = 48m; find the length CD.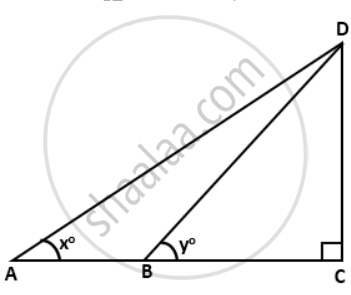
Evaluate the following: `(tan12°)/(cot78°)`
