Advertisements
Advertisements
प्रश्न
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE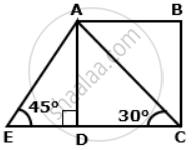
उत्तर

a. In right ΔADC,
tan30° = `"AD"/"DC"`
⇒ `(1)/sqrt(3) = (1.5)/"DC"`
⇒ DC = `1.5sqrt(3)`
Since AB || DC and AD ⊥ EC, ABCD is a parallelogram and hence opposite sides are equal.
⇒ AB
= DC
= `1.5sqrt(3)"cm"`.
b. In right ΔADC,
sin30° = `"AD"/"AC"`
⇒ `(1)/(2) = (1.5)/"AC"`
⇒ AC
= 2 x 1.5
= 3cm.
c. In right ΔADE,
sin45° = `"AD"/"AE"`
⇒ `(1)/sqrt(2) = (1.5)/"AE"`
⇒ AE = `1.5sqrt(2)`.
APPEARS IN
संबंधित प्रश्न
Calculate the value of A, if (sin A - 1) (2 cos A - 1) = 0
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Solve for x : cos2 30° + cos2 x = 1
If θ = 30°, verify that: sin 3θ = 4sinθ . sin(60° - θ) sin(60° + θ)
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ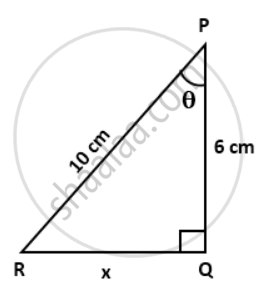
Find the value of 'x' in each of the following: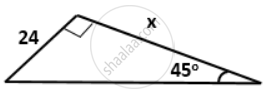
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
