Advertisements
Advertisements
प्रश्न
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
उत्तर
cos3θ = sin(θ - 34°)
⇒ sin(90° - 3θ) = sin(θ - 34°)
⇒ 90° - 3θ = θ - 34°
⇒ 4θ = 124°
⇒ θ = 31°.
APPEARS IN
संबंधित प्रश्न
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
If sin x + cos y = 1 and x = 30°, find the value of y
Solve for x : cos2 30° + sin2 2x = 1
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
Find the value of 'x' in each of the following: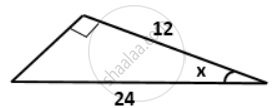
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE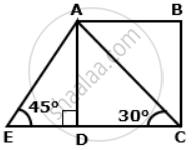
Find:
a. BC
b. AD
c. AC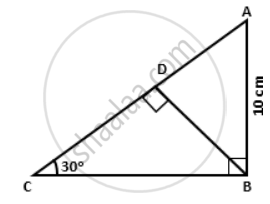
Find the value 'x', if: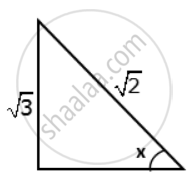
The perimeter of a rhombus is 100 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
