Advertisements
Advertisements
प्रश्न
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
उत्तर
(i) 2 sin x° – 1 = 0
∴ sin x° = `(1)/(2)`
(ii) sin x° = `(1)/(2)`
sin x° = sin 30°
∴ x° = 30°
(iii) cos x° = cos 30° = `(sqrt3)/2`
tax x° = tan 30° = `(1)/(sqrt3)`
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
Find the value of 'A', if cot 3A = 1
Solve for 'θ': `sin θ/(3)` = 1
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
In a rectangle ABCD, AB = 20cm, ∠BAC = 60°, calculate side BC and diagonals AC and BD.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE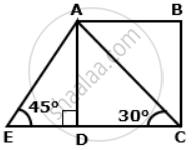
Find the value 'x', if: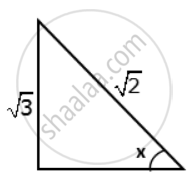
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Evaluate the following: sin35° sin45° sec55° sec45°
If cosθ = sin60° and θ is an acute angle find the value of 1- 2 sin2θ
