Advertisements
Advertisements
Question
Solve for x : sin2 x + sin2 30° = 1
Sum
Solution
sin2x + sin230° = 1
sin2x = 1 –sin2 30°
sin2x = 1 – `(1)/(4)`
sin2x = `(sqrt3)/(2)`
x = 60°
shaalaa.com
Trigonometric Equation Problem and Solution
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Solve for x : cos2 30° + sin2 2x = 1
Find the value of 'A', if `sqrt(3)cot"A"` = 1
Find the value of: `sqrt((1 - sin^2 60°)/(1 + sin^2 60°)` If 3 tan2θ - 1 = 0, find the value
a. cosθ
b. sinθ
Find:
a. BC
b. AD
c. AC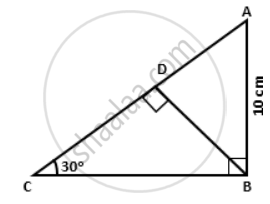
Evaluate the following: `(sec34°)/("cosec"56°)`
Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`
Evaluate the following: tan(78° + θ) + cosec(42° + θ) - cot(12° - θ) - sec(48° - θ)
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
