Advertisements
Advertisements
Question
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
Solution
(i) 2 cos 2A = `sqrt3`
cos 2A = `(sqrt3)/(2)`
cos 2A = cos 30°
2A = 30°
A = 15°
(ii) sin 3A = sin 3(15°)
= sin 45°
= `(1)/(sqrt2)`
(iii) sin2(75° – A ) + cos2 (45 + A) = sin2 ( 75° –15°) + (cos2 ( 45° + 15°)
= sin2 60° + cos2 60°
= `(sqrt3/2)^2 + (1/2)^2`
= `(3)/(4) + (1)/(4)`
= 1
APPEARS IN
RELATED QUESTIONS
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
Solve the following equation for A, if sec 2A = 2
If θ = 30°, verify that: tan2θ = `(2tanθ)/(1 - tan^2θ)`
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos 3θ
If tan x° = `(5)/(12) . tan y° = (3)/(4)` and AB = 48m; find the length CD.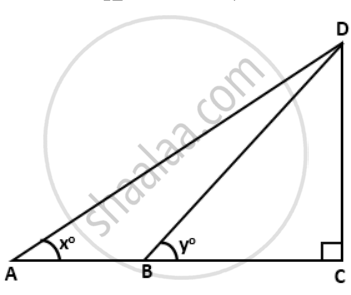
Evaluate the following: `(sin62°)/(cos28°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
