Advertisements
Advertisements
प्रश्न
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
उत्तर
(i) 2 cos 2A = `sqrt3`
cos 2A = `(sqrt3)/(2)`
cos 2A = cos 30°
2A = 30°
A = 15°
(ii) sin 3A = sin 3(15°)
= sin 45°
= `(1)/(sqrt2)`
(iii) sin2(75° – A ) + cos2 (45 + A) = sin2 ( 75° –15°) + (cos2 ( 45° + 15°)
= sin2 60° + cos2 60°
= `(sqrt3/2)^2 + (1/2)^2`
= `(3)/(4) + (1)/(4)`
= 1
APPEARS IN
संबंधित प्रश्न
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Solve the following equations for A, if `sqrt3` tan A = 1
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Find the value of 'A', if 2cos 3A = 1
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.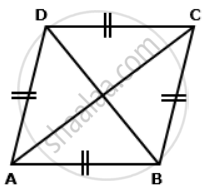
Find the length of EC.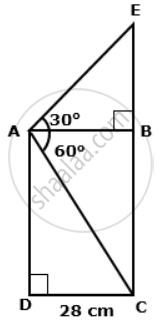
Find the value 'x', if: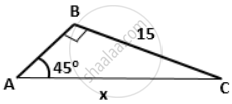
Evaluate the following: sin28° sec62° + tan49° tan41°
