Advertisements
Advertisements
प्रश्न
Find the value of 'A', if 2cos 3A = 1
उत्तर
2cos 3A = 1
⇒ cos 3A = `(1)/(2)`
⇒ cos 3A = cos60°
⇒ 3A = 60°
⇒ A = 20°.
APPEARS IN
संबंधित प्रश्न
Calculate the value of A, if (tan A - 1) (cosec 3A - 1) = 0
Solve for x : cos (2x - 30°) = 0
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
Find the value of 'A', if (2 - cosec 2A) cos 3A = 0
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
In the given figure; ∠B = 90°, ∠ADB = 30°, ∠ACB = 45° and AB = 24 m. Find the length of CD.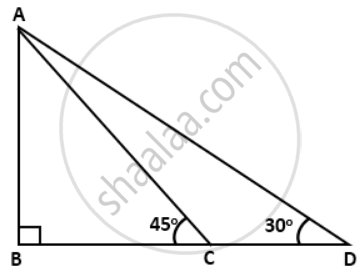
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
Prove the following: sin58° sec32° + cos58° cosec32° = 2
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
