Advertisements
Advertisements
प्रश्न
In the given figure; ∠B = 90°, ∠ADB = 30°, ∠ACB = 45° and AB = 24 m. Find the length of CD.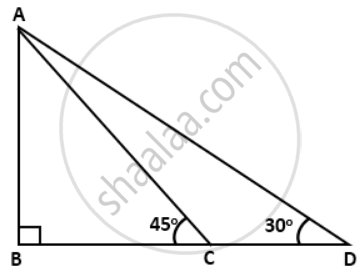
उत्तर

In right ΔABC,
tan45° = `"AB"/"BC"`
⇒ 1 = `(24)/"BC"`
⇒ BC = 24m.
In right ΔABD,
tan 30° = `"AB"/"BD"`
⇒ `(1)/sqrt(3) = (24)/"BD"`
⇒ BD = `24sqrt(3)"m"`
Now,
CD = BD - BC
= `24sqrt(3) - 24`
= `24(sqrt(3) - 1)"m"`.
APPEARS IN
संबंधित प्रश्न
If sin x + cos y = 1 and x = 30°, find the value of y
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
Solve the following equation for A, if tan 3 A = 1
Solve the following equation for A, if 2 sin A = 1
If 3 tan A - 5 cos B = `sqrt3` and B = 90°, find the value of A
Find the value of 'A', if 2 cos A = 1
Find the value of: `sqrt((1 - sin^2 60°)/(1 + sin^2 60°)` If 3 tan2θ - 1 = 0, find the value
a. cosθ
b. sinθ
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
Evaluate the following: `(sin25° cos43°)/(sin47° cos 65°)`
