Advertisements
Advertisements
प्रश्न
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
उत्तर
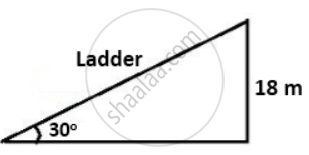
Suppose the length of ladder is x m.
From the figure, we have
`(18)/x` = sin30° ....`[∵ sin = "Perpendicular"/"Hypotenuse"]`
⇒ `(18)/x = (1)/(2)`
⇒ x = 36
Thus, the length of ladder is 36m.
APPEARS IN
संबंधित प्रश्न
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
Solve for x : 2 cos (3x - 15°) = 1
Solve for x : cos2 30° + cos2 x = 1
If sin α + cosβ = 1 and α= 90°, find the value of 'β'.
Find the value 'x', if: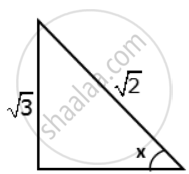
Evaluate the following: sin28° sec62° + tan49° tan41°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
Evaluate the following: cos39° cos48° cos60° cosec42° cosec51°
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
If A + B = 90°, prove that `(tan"A" tan"B" + tan"A" cot"B")/(sin"A" sec"B") - (sin^2"B")/(cos^2"A")` = tan2A
