Advertisements
Advertisements
प्रश्न
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
उत्तर
Given: θ = 30°
cos2θ = cos2 x 30° = cos60° = `(1)/(2)`
`(1 - tan^2 θ )/(1 + tan^2 θ )`
= `(1 - tan^2 30°)/(1 + tan^2 30°)`
= `(1 - (1/sqrt(3))^2)/(1 + (1/sqrt(3))^2)`
= `(1 - 1/3)/(1 + 1/3)`
= `(2/3)/(4/3)`
= `(1)/(2)`
cos4θ - sin4θ = cos430° - sin430°
= `(sqrt(3)/2)^4 - (sqrt(1)/2)^4`
= `(9)/(16) - (1)/(16)`
= `(8)/(16)`
= `(1)/(2)`
2cos2θ - 1 = 2cos230° - 1
= `2(sqrt(3)/2)^2 - 1`
= `2 xx (3)/(4) - 1`
= `(3)/(2) - 1`
= `(1)/(2)`
1 - 2sin2θ = 1 - 2sin230°
= `1 - 2(1/2)^2`
= `1 - 2 xx (1)/(4)`
= `1 - (1)/(2)`
= `(1)/(2)`
⇒ cos2θ
= `(1 - tan^2 θ)/(1 + tan^2 θ)`
= cos4θ - sin4θ
= 2cos2θ - 1
= 1 - 2sin2θ .
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.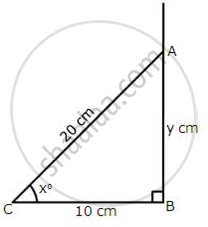
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ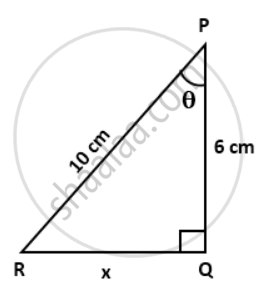
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE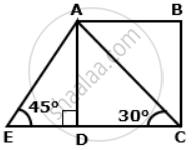
Find the value 'x', if:
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
Prove the following: sin230° + cos230° = `(1)/(2)sec60°`
