Advertisements
Advertisements
प्रश्न
If θ = 30°, verify that: sin2θ = `(2tanθ)/(1 ++ tan^2θ)`
उत्तर
Given: θ = 30°
L.H.S.
= sin2θ
= sin2 x 30°
= sin60°
= `sqrt(3)/(2)`
R.H.S.
= `(2tanθ)/(1 + tan^2θ)`
= `(2tan30°)/(1 + tan^2 30°)`
= `(2 xx 1/sqrt(3))/(1 + (1/sqrt(3))^2`
= `(2/sqrt(3))/(1 + 1/3)`
= `((2)/sqrt(3))/(4/3)`
= `(2)/sqrt(3) xx (3)/(4)`
= `sqrt(3)/(2)`
⇒ L.H.S. = R.H.S.
⇒ sin2θ = `(2tanθ)/(1 + tan^2 θ)`.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if 2 sin 3 A = 1
Solve for 'θ': cot2(θ - 5)° = 3
If tanθ= cotθ and 0°≤ θ ≤ 90°, find the value of 'θ'.
If θ = 30°, verify that: sin 3θ = 4sinθ . sin(60° - θ) sin(60° + θ)
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
Find x and y, in each of the following figure: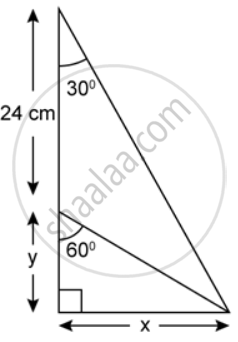
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
Evaluate the following: `(2sin25° sin35° sec55° sec65°)/(5tan 29° tan45° tan61°) + (3cos20° cos50° cot70° cot40°)/(5tan20° tan50° sin70° sin40°)`
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
Prove the following: sin230° + cos230° = `(1)/(2)sec60°`
