Advertisements
Advertisements
प्रश्न
Find x and y, in each of the following figure: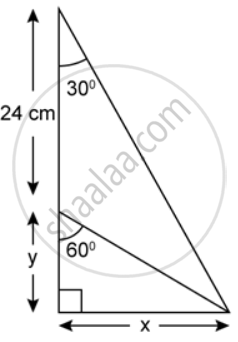
उत्तर
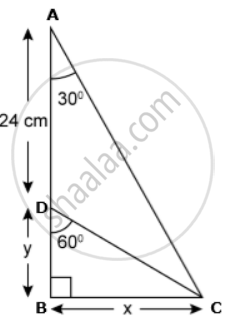
In right ΔABC,
tan30° = `"BC"/"AB"`
⇒ `(1)/sqrt(3) = x/(24 + y)` ....(i)
In right ΔDBC,
tan60° = `"BC"/"DB"`
⇒ `sqrt(3) = x/y`
⇒ x = `sqrt(3)y`
Substituting the value of x in (i), we get
`(1)/sqrt(3) = sqrt(3)/(24 + y)`
⇒ 24 + y = 3y
⇒ 2y = 24
⇒ y = 12cm
⇒ x = `sqrt(3) xx 12 = 12sqrt(3)"cm"`.
APPEARS IN
संबंधित प्रश्न
Solve for x : cos2 30° + sin2 2x = 1
Find the value of 'A', if 2 sin 2A = 1
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
If `sqrt(3)`sec 2θ = 2 and θ< 90°, find the value of θ
In a right triangle ABC, right angled at C, if ∠B = 60° and AB = 15units, find the remaining angles and sides.
Find the value of 'x' in each of the following: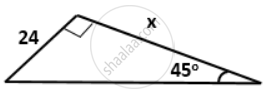
Evaluate the following: `(tan12°)/(cot78°)`
Evaluate the following: `(sec32° cot26°)/(tan64° "cosec"58°)`
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
