Advertisements
Advertisements
प्रश्न
Find x and y, in each of the following figure: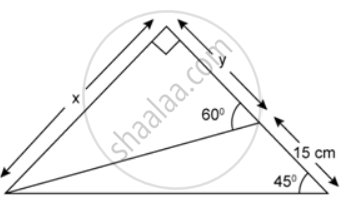
उत्तर
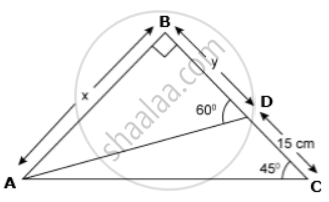
In right ΔABC,
tan45° = `"AB"/"BC"`
⇒ 1 = `x/(15 + y)`
⇒ x = 15 + y ....(i)
In right ΔABD,
tan60° = `"AB"/"BD"`
⇒ `sqrt(3) = x/y`
⇒ `sqrt(3) = (15 + y)/y` ....[From (i)]
⇒ `sqrt(3)y` = 15 + y
⇒ `sqrt(3)y - y` = 15
⇒ `y(sqrt(3) - 1)` = 15
⇒ y = `(15)/(sqrt(3) - 1)`
⇒ y = `(15)/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1`
= `(15(sqrt(3) + 1))/(3 - 1)`
= `(15(sqrt(3) + 1))/(2)"cm"`
⇒ x = `15 + (15(sqrt(3) + 1))/(2)`
= `(30 + 15(sqrt(3) + 1))/(2)`
= `(15(2 + sqrt(3) + 1))/(2)`
= `(15(3 + sqrt(3)))/(2)`
= `(15sqrt(3)(sqrt(3) + 1))/(2)`.
APPEARS IN
संबंधित प्रश्न
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Solve for x : 2 cos (3x - 15°) = 1
Solve for 'θ': `sin θ/(3)` = 1
Find the value 'x', if: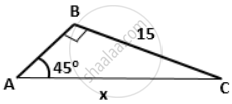
In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:
a. the height of the rocket when it is at point R.
b. the horizontal distance of point S from P.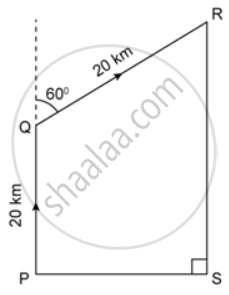
Evaluate the following: `(sin62°)/(cos28°)`
Evaluate the following: `(tan12°)/(cot78°)`
Evaluate the following: `(sec32° cot26°)/(tan64° "cosec"58°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
Evaluate the following: cot20° cot40° cot45° cot50° cot70°
