Advertisements
Advertisements
Question
Find x and y, in each of the following figure: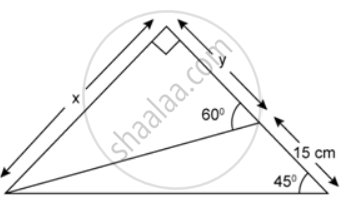
Advertisements
Solution
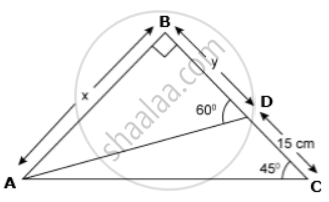
In right ΔABC,
tan45° = `"AB"/"BC"`
⇒ 1 = `x/(15 + y)`
⇒ x = 15 + y ....(i)
In right ΔABD,
tan60° = `"AB"/"BD"`
⇒ `sqrt(3) = x/y`
⇒ `sqrt(3) = (15 + y)/y` ....[From (i)]
⇒ `sqrt(3)y` = 15 + y
⇒ `sqrt(3)y - y` = 15
⇒ `y(sqrt(3) - 1)` = 15
⇒ y = `(15)/(sqrt(3) - 1)`
⇒ y = `(15)/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1`
= `(15(sqrt(3) + 1))/(3 - 1)`
= `(15(sqrt(3) + 1))/(2)"cm"`
⇒ x = `15 + (15(sqrt(3) + 1))/(2)`
= `(30 + 15(sqrt(3) + 1))/(2)`
= `(15(2 + sqrt(3) + 1))/(2)`
= `(15(3 + sqrt(3)))/(2)`
= `(15sqrt(3)(sqrt(3) + 1))/(2)`.
APPEARS IN
RELATED QUESTIONS
If 4 sin2 θ – 1 = 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2 θ.
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
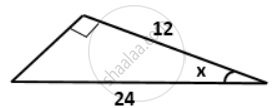
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:
a. the height of the rocket when it is at point R.
b. the horizontal distance of point S from P.
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
If sin(θ - 15°) = cos(θ - 25°), find the value of θ if (θ-15°) and (θ - 25°) are acute angles.
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
