Advertisements
Advertisements
Question
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
Solution
`sec(θ/2 + 10°) = (2)/sqrt(3)`
⇒ `sec(θ/2 + 10°)` = sec 30°
⇒ `θ/(2) + 10°` = 30°
⇒ `θ/(2)` = 20°
⇒ θ = 40°.
APPEARS IN
RELATED QUESTIONS
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Solve the following equations for A, if `sqrt3` tan A = 1
Find the value of 'A', if 2cos 3A = 1
If θ = 30°, verify that: sin2θ = `(2tanθ)/(1 ++ tan^2θ)`
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
Find x and y, in each of the following figure: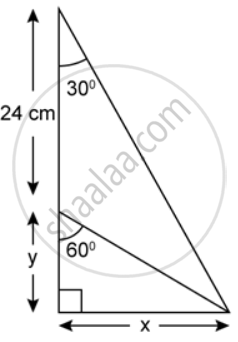
Evaluate the following: `(sin62°)/(cos28°)`
Evaluate the following: sin28° sec62° + tan49° tan41°
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
