Advertisements
Advertisements
Question
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
Solution
`(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
= `(5cot(90° - 85°) cot(90° - 75°) cot(90° - 65°) cot(90° - 55°) xx 1)/(7 xx 1xx tan55° tan65° tan75° tan85°) + (2"cosec"(90° - 78°) "cosec"(90° - 66°) cos78° cos66°)/(7sin(90° - 76°) sin(90° - 67°) sec76° sec67°)`
= `(5tan85° tan75° tan65° tan55°)/(7 xx tan55° tan65° tan75° tan85°) + (2sec78° sec66° xx 1/(sec78°) xx 1/(sec66°))/(7cos76° cos67° xx 1/(cos76°) xx 1/(cos67°)`
= `(5)/(7) + (2)/(7)`
= `(7)/(7)`
= 1.
APPEARS IN
RELATED QUESTIONS
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Solve for x : sin2 x + sin2 30° = 1
Find the value of 'A', if cot 3A = 1
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
Find the value of 'x' in each of the following: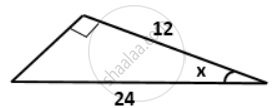
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Evaluate the following: `(sec32° cot26°)/(tan64° "cosec"58°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin53° + sec66° - sin50°
