Advertisements
Advertisements
Question
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Solution
cos 3A (2 sin 2A – 1) = 0
cos 3A = 0 and 2 sin 2A – 1 = 0
cos 3A = cos90° and 2 sin 2A = 1
3A = 90° and sin 2A = `(1)/(2)`
A = 30° and sin 2A = sin 30°
A = 30°
2A = 30°
⇒ A = 15°
APPEARS IN
RELATED QUESTIONS
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
If sin 3A = 1 and 0 < A < 90°, find cos 2A
If ΔABC is a right triangle such that ∠C = 90°, ∠A = 45° and BC =7units, find ∠B, AB and AC.
Find the length of EC.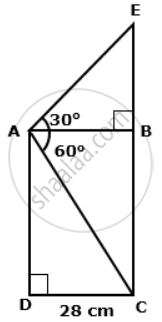
Evaluate the following: `(sin62°)/(cos28°)`
Evaluate the following: cot27° - tan63°
Evaluate the following: sin35° sin45° sec55° sec45°
Evaluate the following: sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
