Advertisements
Advertisements
Question
Evaluate the following: sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
Solution
sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
= sin[90° - (55° - θ)] - cos(55° - θ) - tan[90° - (48° - θ)] + cot(48° - θ)
= cos(55° - θ) - cos(55° - θ) - cot(48° - θ) + cot(48° - θ)
= 0.
APPEARS IN
RELATED QUESTIONS
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ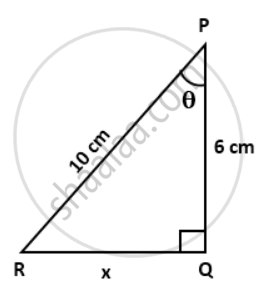
In a right triangle ABC, right angled at C, if ∠B = 60° and AB = 15units, find the remaining angles and sides.
Find the value of 'x' in each of the following: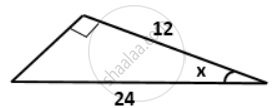
Find the value 'x', if:
Evaluate the following: sin31° - cos59°
Evaluate the following: cosec 54° - sec 36°
Evaluate the following: cot20° cot40° cot45° cot50° cot70°
