Advertisements
Advertisements
Question
Find the value 'x', if:
Solution

BEDC is a rectangle.
⇒ BE
= DC
= `60sqrt(3)"m"`
In right ΔAEB,
tan30° = `"AE"/"BE"`
⇒ `(1)/sqrt(3) = "AE"/(60sqrt(3)`
⇒ AE = 60m
Now,
x = AD = AE + ED
= 60 + 15
= 75m.
APPEARS IN
RELATED QUESTIONS
State for any acute angle θ whether sin θ increases or decreases as θ increases
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.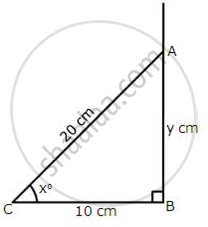
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
Find the magnitude of angle A, if 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
Find the value of 'x' in each of the following: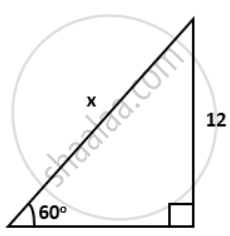
Find:
a. BC
b. AD
c. AC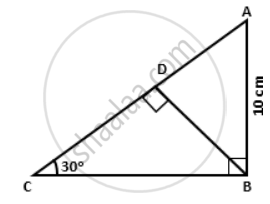
Evaluate the following: `(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
If sin(θ - 15°) = cos(θ - 25°), find the value of θ if (θ-15°) and (θ - 25°) are acute angles.
