Advertisements
Advertisements
Question
If sin(θ - 15°) = cos(θ - 25°), find the value of θ if (θ-15°) and (θ - 25°) are acute angles.
Solution
sin(θ - 15°) = cos(θ - 25°)
⇒ cos[90° - (θ - 15°)] = cos(θ - 25°)
⇒ 90° - (θ - 15°) = θ - 25°
⇒ 105° - θ = θ - 25°
⇒ 2θ = 130°
⇒ θ = 65°.
APPEARS IN
RELATED QUESTIONS
Calculate the value of A, if (sin A - 1) (2 cos A - 1) = 0
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
If θ = 30°, verify that: sin2θ = `(2tanθ)/(1 ++ tan^2θ)`
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB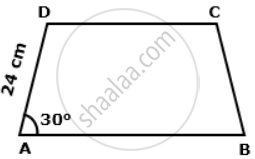
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
Prove the following: sin58° sec32° + cos58° cosec32° = 2
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
