If P, Q and R are the interior angles of ΔPQR, prove that cot ( Q + R 2 ) = tan P 2 - Mathematics

If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`

Sum

Since P, Q and R are interior angles of ΔPQR,
P + Q + R = 180°
⇒ Q + R = 180° - P
Now,
L.H.S. = `cot (("Q" + "R")/2)`

= `cot ((180° - "P")/2)`

= `cot(90° - "P"/2)`

= `tan "P"/(2)`
= R.H.S.

shaalaa.com

Trigonometric Equation Problem and Solution

Is there an error in this question or solution?

Chapter 27: Trigonometrical Ratios of Standard Angles - Exercise 27.3

Chapter 27 Trigonometrical Ratios of Standard Angles
Exercise 27.3 | Q 11

If sin 3A = 1 and 0 < A < 90^°, find cos 2A

Solve for x : cos `(x)/(3) –1` = 0

Find the value of: `sqrt((1 - sin^2 60°)/(1 + sin^2 60°)` If 3 tan²θ - 1 = 0, find the value
a. cosθ
b. sinθ

Find the value 'x', if: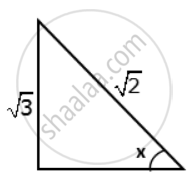

Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.

Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`

Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`

Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`

Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)

Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos²θ