Advertisements
Advertisements
Question
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
Solution
Since A, B and C are interior angles of ΔABC,
A + B + C = 180°
⇒ A + B = 180° - C
Now,
L.H.S. = `sin (("A" + "B")/2)`
= `sin ((180° - "C")/2)`
= `sin(90° - "C"/2)`
= `cos "C"/(2)`
= R.H.S.
APPEARS IN
RELATED QUESTIONS
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
If sin α + cosβ = 1 and α= 90°, find the value of 'β'.
Solve for 'θ': cot2(θ - 5)° = 3
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
If `sqrt(3)`sec 2θ = 2 and θ< 90°, find the value of θ
Find the value of 'x' in each of the following: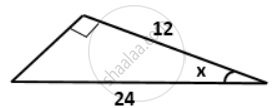
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.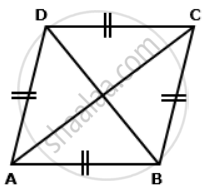
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
Evaluate the following: `(5sec68°)/("cosec"22°) + (3sin52° sec38°)/(cot51° cot39°)`
