Advertisements
Advertisements
Question
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Solution
4 sin2 θ – 1 = 0
sin2 θ = `(1)/(4)`
sin θ = `(1)/(2)`
sin θ = sin30°
θ = 30°
cos2 θ + tan2 θ= cos230° + tan230°
= `(sqrt3/2)^2 + ( 1/sqrt3)^2`
= `(3)/(4) + (1)/(3)`
= `(9 + 4)/(12)`
= `(13)/(12)`
APPEARS IN
RELATED QUESTIONS
State for any acute angle θ whether sin θ increases or decreases as θ increases
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
Find the value of 'A', if (2 - cosec 2A) cos 3A = 0
If tanθ= cotθ and 0°≤ θ ≤ 90°, find the value of 'θ'.
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
In the given figure, if tan θ = `(5)/(13), tan α = (3)/(5)` and RS = 12m, find the value of 'h'.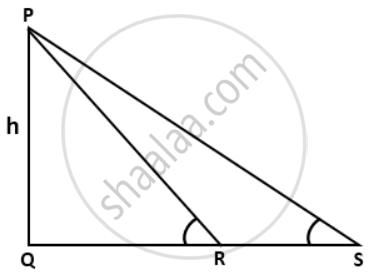
Find x and y, in each of the following figure: