Advertisements
Advertisements
Question
Find the value of 'A', if (2 - cosec 2A) cos 3A = 0
Solution
(2 - cosec 2A) cos 3A = 0
⇒ 2 - cosec 2A = 0 and cos 3A = 0
⇒ cosec 2A = 2 and cos 3A = 0
⇒ cosec 2A = cosec 30° and cos 3A = cos 90°
⇒ 2A = 30° and 3A = 90°
⇒ A = 15° and A = 30°.
APPEARS IN
RELATED QUESTIONS
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
If θ < 90°, find the value of: sin2θ + cos2θ
Find the value of 'x' in each of the following: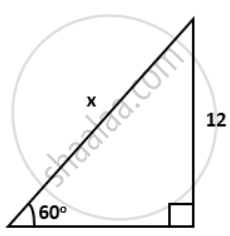
Evaluate the following: `(sec34°)/("cosec"56°)`
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
