Advertisements
Advertisements
Question
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
Solution
2θ = 30°
⇒ θ = 15°
∴ `(sin3θ - 2sin4θ)/(cos3θ - 2cos4θ)`
= `(sin3 xx 15° - 2sin4 xx 15°)/(cos3 xx 15° - 2cos"4 xx 15°)`
= `"(sin45° - 2sin60°)/(cos45° - 2cos60°)`
= `(1/sqrt(2) - 2 xx sqrt(3)/(2))/((1)/sqrt(2) - 2 xx (1)/(2))`
= `(1/sqrt(2) - sqrt(3))/(1/sqrt(2) - 1)`
= `((1 - sqrt(6))/(sqrt(2)))/((1 - sqrt(2))/(sqrt(2)`
= `(1 - sqrt(6))/(1 - sqrt(2))`
= `(1 - sqrt(6))/(1 - sqrt(2)) xx (1 + sqrt(2))/(1 + sqrt(2)`
= `(1 + sqrt(2) - sqrt(6) - sqrt12)/(1 - 2)`
= `(1 + sqrt(2) - sqrt(6) - 2sqrt(3))/(-1)`
= `2sqrt(3) + sqrt(6) - sqrt(2) - 1`.
APPEARS IN
RELATED QUESTIONS
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.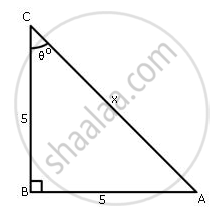
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
Solve for 'θ': cot2(θ - 5)° = 3
If θ = 30°, verify that: sin 3θ = 4sinθ . sin(60° - θ) sin(60° + θ)
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
Find the value of 'x' in each of the following: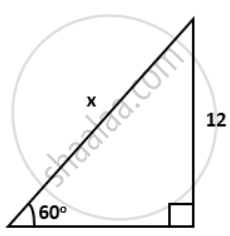
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE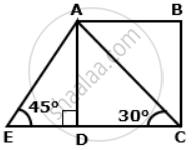
Find the value 'x', if: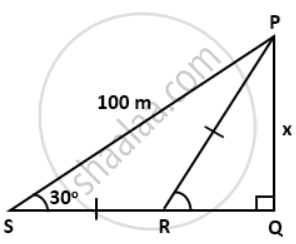
Evaluate the following: `(tan12°)/(cot78°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
